理解word2vec
最近在看斯坦福的课程,对word2vec有了更深刻的理解,在这里总结一下。
什么是word2vec
传统的one hot的表达方式维度太大,并且无法表达词之间的语义之间的联系
word2vec原理(skip - gram来举例)
skip gram是使用中心词预测背景词的概率,架构图如下: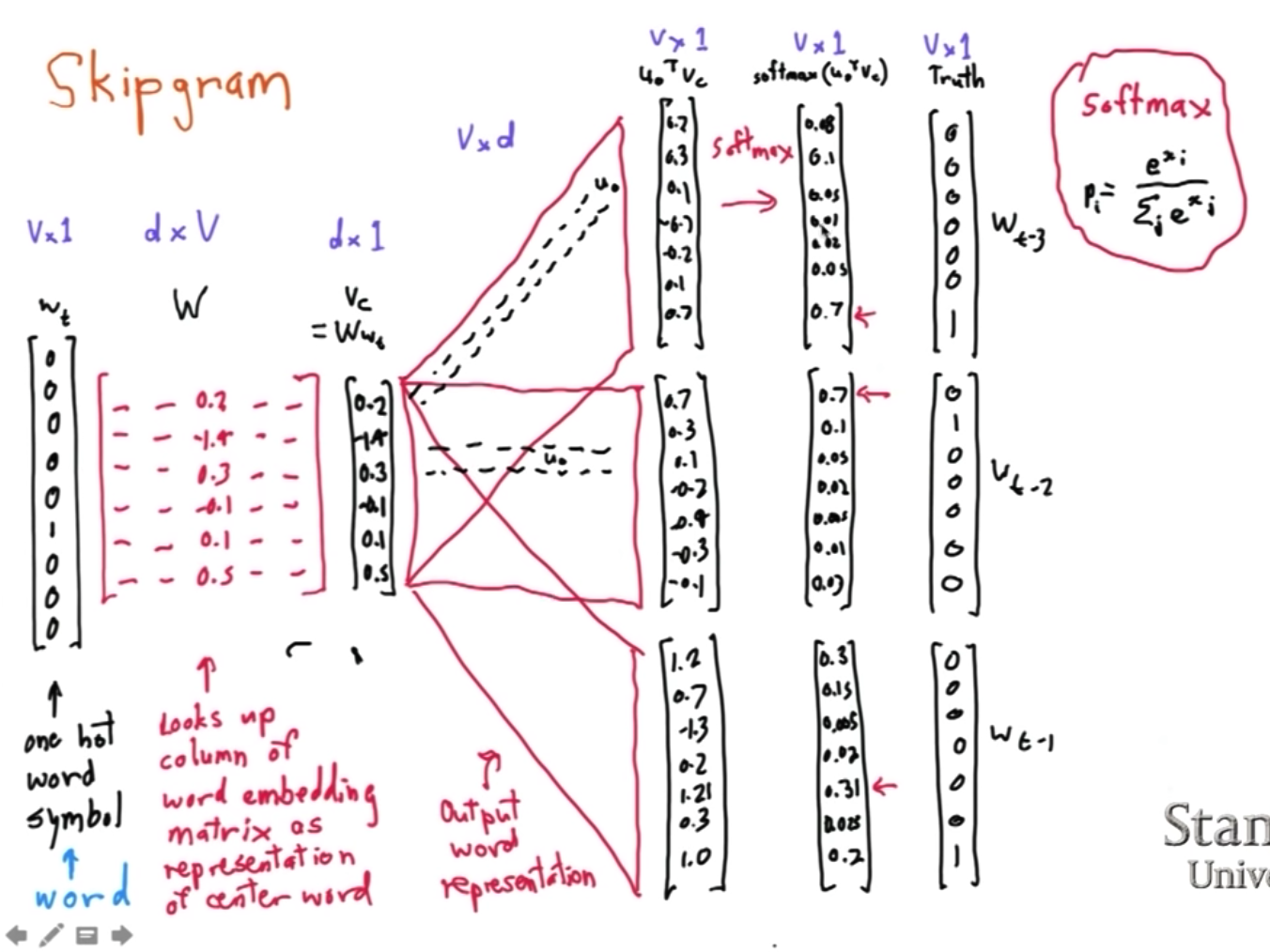
我们使用最大似然估计来写出整体要优化的目标:
$\prod_{t=1}^{T}\prod_{-m <= j <= m, j \neq 0}p(w_{t+j} | w_t; \theta)$
其中:m表示窗口大小,T表示总共有T个window
我们将最大似然转换为loss function只需要取-log,之后的结果为:
$J(\theta) = - \frac{1}{T} \sum_{t=1}^{T} \sum_{-m <= j <= m, j \neq 0 }\log {p(w_{t+j} | w_t)}$
$p(o|c) = \frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{v} \exp (u_w^Tv_c)}$,这里使用softmax对概率进行了归一化。
c表示中心词索引,o表示背景词索引,$u_o$和$v_c$分别是对应的向量表示。这里让我先想到了fm也是对每个特征转换成了一个向量表示,然后求内积的inner product。
如何求解参数
对中心词$v_c$求导
$\frac{\partial \log{\frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{v} \exp (u_w^T v_c)}}}{\partial v_c}$
$=\frac{\partial \lgroup \log{ {\exp(u_o^T v_c)} - \log{ \sum_{w=1}^{v} \exp (u_w^Tv_c) } \rgroup } } {\partial v_c}$
$=\frac{\partial \log{\exp(u_o^Tv_c)} } {\partial v_c} - \frac { \partial \log{\sum_{w=1}^{v} \exp (u_w^Tv_c)} } {\partial v_c}$
$= u_o - {\frac{1}{ \sum_{w=1}^{v} exp(u_w^Tv_c) } } \frac { \partial { \sum_{x=1}^{v} \exp (u_x^Tv_c) } } { \partial v_c }$
$= u_o - {\frac{1} { \sum_{w=1}^{v} exp(u_w^Tv_c) } } { { \sum_{x=1}^{v} \frac {\partial {\exp (u_x^Tv_c)} } {\partial v_c} } }$
$= u_o - {\frac{1} { \sum_{w=1}^{v} exp(u_w^Tv_c) } } { { \sum_{x=1}^{v} \exp (u_x^Tv_c) u_x} }$
$= u_o - { { } } { { \sum_{x=1}^{v} \frac {\exp (u_x^Tv_c)} {\sum_{w=1}^{v} exp(u_w^Tv_c)} u_x} }$
$=u_o - \sum_{x=1}^{v} p(x|c) u_x$
问题:比如一个句子 a1 a2 a3 a4 a5,5个term构成,窗口为1;a2这个term既可以作为中心词,也可以作为背景词,需要注意的是,a2这个term作为中心词和背景词的vector是不一样的,更新的不是一个vector。
负采样
基础
$\sigma(-x) = 1 - \sigma(x)$
$\sigma(x) = \frac {1} {1 + e^{-x}}$
定义
如果考虑整个V集合的负样本,计算量太大,因此提出了负采样的方法
$J(\theta) = \frac{1}{T} \sum_{t=1}^{T}J_t(\theta)$
$J_t(\theta) = log{\sigma(u_o^Tv_c)} + \sum_{j=1}^{k}E_{j \sim P(w)}[log{\sigma(-u_j^Tv_c)}]$
其中 k 表示从分布$P(w)$中随机负采样出的负例个数,t表示第t个window
推倒
D=1 表示中心词$w_c$和背景词$w_o$同时出现在一个窗口内
D=0 表示中心词$w_c$和背景词$w_o$没有同时出现在一个窗口内
转换成了二分类的问题
$P(D=1| w_o, w_c) = \sigma(u_{o}^{T}v_c)$
$P(D = 0 |w_o, w_c) = 1 - P(D = 1 | w_o, w_c) = \sigma(-u_{o}^{T}v_c)$
最大似然估计可以转化为:
$P(w_o | w_c) = P(D=1|w_o, w_c) \prod_{j=1, w_j \sim P(w) }^{k}P(D=0|w_j, w_c)$
取-log后即为最终的loss function。